12.2 Vectors in the Plane
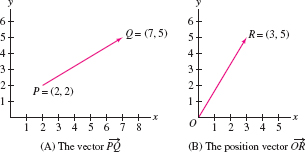
A two-dimensional vector \(\textbf{v}\) is determined by two points in the plane: an initial point \(P\) (also called the “tail” or basepoint) and a terminal point \(Q\) (also called the “head”). We write \[\textbf{v} = \overrightarrow{PQ}\]
and we draw \(\textbf{v}\) as an arrow pointing from \(P\) to \(Q\). This vector is said to be based at \(P\). Figure 12.1 shows the vector with initial point \(P = (2,2)\) and terminal point \(Q = (7, 5)\). The length or magnitude of \(\textbf{v}\), denoted \(\parallel{\textbf{v}}\parallel\), is the distance from \(P\) to \(Q\).
The vector \(\textbf{v} = \overrightarrow{OR}\) pointing from the origin to a point \(R\) is called the position vector of \(R\). Figure 12.1 shows the position vector of the point \(R = (3,5)\).
NOTATION
In this text, vectors are represented by boldface lowercase letters such as \(\textbf{v}\), \(\textbf{w}\), \(\textbf{a}\), \(\textbf{b}\), etc.
We now introduce some vector terminology.
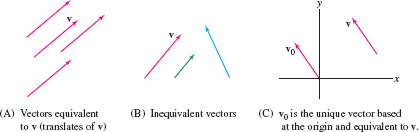
- Two vectors \(\textbf{v}\) and \(\textbf{w}\) of nonzero length are called parallel if the lines through \(\textbf{v}\) and \(\textbf{w}\) are parallel. Parallel vectors point either in the same or in opposite directions [Figure 12.2].
- A vector \(\textbf{v}\) is said to undergo a translation when it is moved parallel to itself without changing its length or direction. The resulting vector \(\textbf{w}\) is called a translate of \(\textbf{v}\) [Figure 12.2]. Translates have the same length and direction but different basepoints.
In many situations, it is convenient to treat vectors with the same length and direction as equivalent, even if they have different basepoints. With this in mind, we say that
- \(\textbf{v}\) and \(\textbf{w}\) are equivalent if \(\textbf{w}\) is a translate of \(\textbf{v}\) [Figure 12.3].

658
Every vector can be translated so that its tail is at the origin [Figure 12.3]. Therefore, \[ \textit {Every vector \(\textbf{v}\) is equivalent to a unique vector \(\textbf{v}_0\) based at the origin}. \]
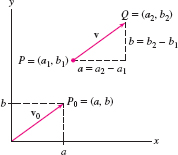
To work algebraically, we define the components of a vector (Figure 12.4).
DEFINITION Components of a Vector
The components of \(\textbf{v}=\overrightarrow{PQ}\), where \(P= (a_1,b_1)\) and \(Q=(a_2,b_2)\), are the quantities \[\boxed{ a = a_2-a_1\quad(\textrm{\(x\)-component}),\qquad b = b_2-b_1\quad(\textrm{\(y\)-component}) }\]
The pair of components is denoted \(\langle a, b\rangle\).
- The length of a vector in terms of its components (by the distance formula, see Figure 12.4) is \[ \boxed{ \parallel{\textbf{v}}\parallel = \parallel{\overrightarrow{PQ}}\parallel = \sqrt{a^2+b^2} } \]
- The zero vector (whose head and tail coincide) is the vector \(\textbf{0} =\langle 0,0\rangle\) of length zero.
The components \(\langle a,b\rangle\) determine the length and direction of \(\textbf{v}\), but not its basepoint. Therefore, two vectors have the same components if and only if they are equivalent. Nevertheless, the standard practice is to describe a vector by its components, and thus we write \[ \textbf{v}=\langle a,b\rangle \]
Although this notation is ambiguous (because it does not specify the basepoint), it rarely causes confusion in practice. To further avoid confusion, the following convention will be in force for the remainder of the text: \[ \boxed{\textit{We assume all vectors are based at the origin unless otherwise stated.}} \]
Note
- In this text, “angle brackets” are used to distinguish between the vector \(\textbf{v} = \langle a,b \rangle\) and the point \(P = (a,b)\). Some textbooks denote both \(\textbf{v}\) and \(P\) by \((a,b)\).
- When referring to vectors, we use the terms “length” and “magnitude” interchangeably. The term “norm” is also commonly used.
EXAMPLE 1
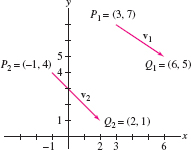
Determine whether \(\textbf{v}_1=\overrightarrow{P_1Q_1}\) and \(\textbf{v}_2=\overrightarrow{P_2Q_2}\) are equivalent, where \[ P_1=(3,7),\quad Q_1 = (6,5)\qquad\textrm{and}\qquad P_2= (-1,4),\quad Q_2=(2,1) \]
What is the magnitude of \(\textbf{v}_1\)?
659
Solution We can test for equivalence by computing the components (Figure 12.5): \begin{align*} \textbf{v}_1 = \langle 6-3, 5-7 \rangle = \langle 3,-2\rangle,\qquad \textbf{v}_2= \langle 2-(-1),1-4\rangle = \langle 3,-3\rangle \end{align*}
The components of \(\textbf{v}_1\) and \(\textbf{v}_2\) are not the same, so \(\textbf{v}_1\) and \(\textbf{v}_2\) are not equivalent. Since \(\textbf{v}_1 = \langle 3, -2\rangle\), its magnitude is \[ \parallel{\textbf{v}_1}\parallel = \sqrt{3^2+(-2)^2} = \sqrt{13} \]
EXAMPLE 2
Sketch the vector \(\textbf{v} = \langle 2, -3\rangle\) based at \(P = (1,4)\) and the vector \(\textbf{v}_0\) equivalent to \(\textbf{v}\) based at the origin.
Solution The vector \(\textbf{v} = \langle 2, -3\rangle\) based at \(P=(1,4)\) has terminal point \(Q = (1 + 2, 4- 3)=(3,1)\), located two units to the right and three units down from \(P\) as shown in Figure 12.6. The vector \(\textbf{v}_0\) equivalent to \(\textbf{v}\) based at \(O\) has terminal point \((2,-3)\).
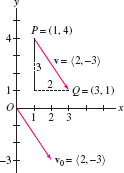
Vector Algebra
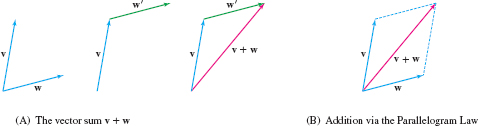
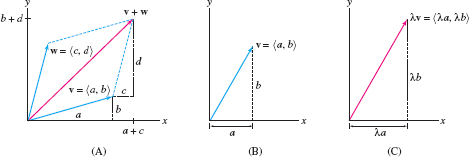
We now define two basic vector operations: vector addition and scalar multiplication. The vector sum \(\textbf{v} + \textbf{w}\) is defined when \(\textbf{v}\) and \(\textbf{w}\) have the same basepoint: Translate \(\textbf{w}\) to the equivalent vector \(\textbf{w}'\) whose tail coincides with the head of \(\textbf{v}\). The sum \(\textbf{v}+\textbf{w}\) is the vector pointing from the tail of \(\textbf{v}\) to the head of \(\textbf{w}'\) [Figure 12.7]. Alternatively, we can use the Parallelogram Law: \(\textbf{v} + \textbf{w}\) is the vector pointing from the basepoint to the opposite vertex of the parallelogram formed by \(\textbf{v}\) and \(\textbf{w}\) [Figure 12.7].
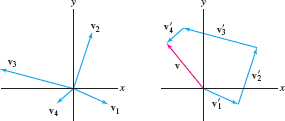
To add several vectors \(\textbf{v}_1, \textbf{v}_2, \dots, \textbf{v}_n\), translate the vectors to \(\textbf{v}_1 = \textbf{v}_1',\textbf{v}'_2, \dots, \textbf{v}'_n\) so that they lie head to tail as in Figure 12.8. The vector sum \(\textbf{v}=\textbf{v}_1+\textbf{v}_2+\cdots +\textbf{v}_n\) is the vector whose terminal point is the terminal point of \(\textbf{v}'_n\).
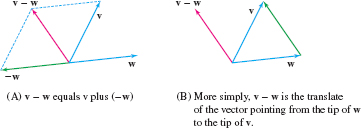
Vector subtraction \(\textbf{v}-\textbf{w}\) is carried out by adding \(-\textbf{w}\) to \(\textbf{v}\) as in Figure 12.9. Or, more simply, draw the vector pointing from \(\textbf{w}\) to \(\textbf{v}\) as in Figure 12.9, and translate it back to the basepoint to obtain \(\textbf{v}-\textbf{w}\).
CAUTION
Remember that the vector \(\textbf{v}-\textbf{w}\) points in the direction from the tip of \(\textbf{w}\) to the tip of \(\textbf{v}\) (not from the tip of \(\textbf{v}\) to the tip of \(\textbf{w}\)).
660
The term scalar is another word for “real number,” and we often speak of scalar versus vector quantities. Thus, the number 8 is a scalar, while \(\langle 8, 2\rangle\) is a vector. If \(\lambda\) is a scalar and \(\textbf{v}\) is a nonzero vector, the scalar multiple \(\lambda \textbf{v}\) is defined as follows (Figure 12.10):
NOTATION
\(\lambda\) (pronounced “lambda”) is the eleventh letter in the Greek alphabet. We use the symbol \(\lambda\) often (but not exclusively) to denote a scalar.
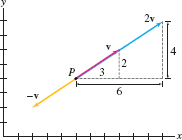
- \(\lambda \textbf{v}\) has length \(|\lambda| \parallel{v}\parallel\).
- It points in the same direction as \(\textbf{v}\) if \(\lambda \gt 0\).
- It points in the opposite direction if \(\lambda \lt 0\).
Note that \(0\textbf{v} = \textbf{0}\) for all \(\textbf{v}\), and \[ \boxed{\parallel{\lambda \textbf{v}} = |\lambda| \parallel{\textbf{v}}\parallel} \]
In particular, \(-\textbf{v}\) has the same length as \(\textbf{v}\) but points in the opposite direction. A vector \(\textbf{w}\) is parallel to \(\textbf{v}\) if and only if \(\textbf{w} = \lambda \textbf{v}\) for some nonzero scalar \(\lambda\).
Vector addition and scalar multiplication operations are easily performed using components. To add or subtract two vectors \(\textbf{v}\) and \(\textbf{w}\), we add or subtract their components. This follows from the parallelogram law as indicated in Figure 12.11.
Similarly, to multiply \(\textbf{v}\) by a scalar \(\lambda\), we multiply the components of \(\textbf{v}\) by \(\lambda\) [Figure 12.11 and Figure 12.11]. Indeed, if \(\textbf{v}=\langle a, b\rangle\) is nonzero, \(\langle \lambda a,\lambda b\rangle\) has length \(|\lambda| \parallel{\textbf{v}}\parallel\). It points in the same direction as \(\langle a,b\rangle\) if \(\lambda \gt 0\), and in the opposite direction if \(\lambda \lt 0\).
Vector Operations Using Components
If \(\textbf{v}= \langle a,b\rangle\) and \(\textbf{w}=\langle c,d\rangle\), then:
- (i) \({\textbf{v}+\textbf{w} = \langle a+c,b+d \rangle}\)
- (ii) \({\textbf{v}-\textbf{w} = \langle a-c,b-d \rangle}\)
- (iii) \({\lambda \textbf{v} = \langle\lambda a, \lambda b \rangle}\)
- (iv) \({\textbf{v}+\textbf{0} =\textbf{0}+\textbf{v}=\textbf{v}}\)
We also note that if \(P=(a_1,b_1)\) and \(Q=(a_2,b_2)\), then components of the vector \(\textbf{v} = \overrightarrow{PQ}\) are conveniently computed as the difference \[ \overrightarrow{PQ} = \overrightarrow{OQ}-\overrightarrow{OP}=\langle a_2,b_2\rangle - \langle a_1,b_1\rangle = \langle a_2 - a_1,b_2-b_1\rangle \]
661
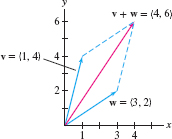
EXAMPLE 3
For \(\textbf{v}=\langle 1,4\rangle\), \(\textbf{w}=\langle 3,2\rangle\), calculate
- (a) \(\textbf{v}+\textbf{w}\)
- (b) \(5\textbf{v}\)
Solution \begin{align*} \textbf{v}+\textbf{w} &=\langle 1,4\rangle + \langle 3,2\rangle = \langle 1+3,4+2\rangle = \langle 4,6\rangle\\ 5\textbf{v} &= 5\langle 1,4\rangle= \langle 5,20\rangle \end{align*}
The vector sum is illustrated in Figure 12.12.
Vector operations obey the usual laws of algebra.
THEOREM 1 Basic Properties of Vector Algebra
For all vectors \(\textbf{u, v, w}\) and for all scalars \(\lambda\),
Commutative Law: \(\textbf{v}+\textbf{w}=\textbf{w}+\textbf{v}\)
Associative Law: \(\textbf{u} +(\textbf{v}+\textbf{w})=(\textbf{u}+\textbf{v})+\textbf{w}\)
Distributive Law for Scalars: \(\lambda (\textbf{v}+\textbf{w})=\lambda\textbf{v}+\lambda\textbf{w}\)
These properties are verified easily using components. For example, we can check that vector addition is commutative: \[ \langle a,b\rangle + \langle c,d\rangle = \underbrace{\langle a+c,b+d\rangle = \langle c+a,d+b\rangle}_{\textrm{Commutativity of ordinary addition}}=\langle c,d\rangle + \langle a,b\rangle \]
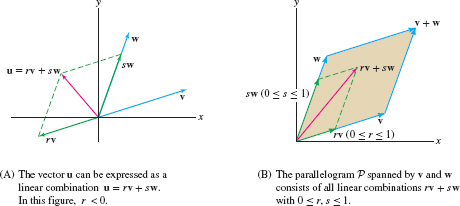
A linear combination of vectors \(\textbf{v}\) and \(\textbf{w}\) is a vector \[ r\textbf{v}+s\textbf{w} \]
where \(r\) and \(s\) are scalars. If \(\textbf{v}\) and \(\textbf{w}\) are not parallel, then every vector \(\textbf{u}\) in the plane can be expressed as a linear combination \(\textbf{u} = r\textbf{v}+s\textbf{w}\) [Figure 12.13]. The parallelogram \(\mathcal P\) whose vertices are the origin and the terminal points of \(\textbf{v}\), \(\textbf{w}\) and \(\textbf{v}+\textbf{w}\) is called the parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\) [Figure 12.13]. It consists of the linear combinations \(r\textbf{v}+s\textbf{w}\) with \(0\le r\le 1\) and \(0\le s\le 1\).
662
EXAMPLE 4 Linear Combinations
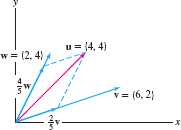
Express the vector \(\textbf{u}=\langle 4,4\rangle\) in Figure 12.14 as a linear combination of \(\textbf{v}=\langle 6,2\rangle\) and \(\textbf{w} = \langle 2,4\rangle\).
Solution We must find \(r\) and \(s\) such that \({r\textbf{v}+s\textbf{w}=\langle 4,4\rangle}\), or \[ r\langle 6,2\rangle + s \langle 2,4\rangle = \langle 6r+2s,2r+4s\rangle = \langle 4,4\rangle \]
The components must be equal, so we have a system of two linear equations: \begin{align*} 6r+2s &= 4\\ 2r+4s &= 4 \end{align*}
Subtracting the equations, we obtain \(4r-2s=0\) or \(s=2r\). Setting \(s=2r\) in the first equation yields \(6r+4r=4\) or \(r=\frac25\), and then \(s = 2r =\frac45\). Therefore, \[ \textbf{u}=\langle 4,4\rangle = \frac25\langle 6,2\rangle + \frac45\langle 2,4\rangle \]
CONCEPTUAL INSIGHT
In general, to write a vector \(\textbf{u}=\langle e, f\rangle\) as a linear combination of two other vectors \(\textbf{v}=\langle a,b\rangle\) and \(\textbf{w}=\langle c, d\rangle\), we have to solve a system of two linear equations in two unknowns \(r\) and \(s\): \[ rv+sw = u \quad\Leftrightarrow\quad r\langle a,b\rangle+s\langle c,d\rangle = \langle e,f\rangle\quad\Leftrightarrow\quad \left\{ ar+cs = e \\ br+ds = \! f \right. \]
On the other hand, vectors give us a way of visualizing the system of equations geometrically. The solution is represented by a parallelogram as in Figure 12.14. This relation between vectors and systems of linear equations extends to any number of variables and is the starting point for the important subject of linear algebra.
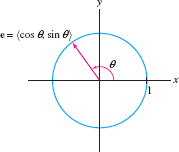
A vector of length 1 is called a unit vector. Unit vectors are often used to indicate direction, when it is not necessary to specify length. The head of a unit vector \(\textbf{e}\) based at the origin lies on the unit circle and has components \[ \textbf{e} = \langle \cos\theta, \sin\theta\rangle \]
where \(\theta\) is the angle between \(\textbf{e}\) and the positive \(x\)-axis (Figure 12.15).
We can always scale a nonzero vector \(\textbf{v}=\langle a,b\rangle\) to obtain a unit vector pointing in the same direction (Figure 12.16): \[ \boxed{\textbf{e}_\textbf{v} = \frac{1}{\parallel{\textbf{v}\parallel}}\textbf{v}} \]
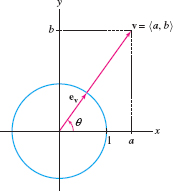
Indeed, we can check that \(\textbf{e}_\textbf{v}\) is a unit vector as follows: \[ \parallel{\textbf{e}_{\textbf{v}}}\parallel = \left\Vert \frac{1}{\parallel{\textbf{v}}\parallel} \textbf{v} \right\Vert = \frac{1}{\parallel{\textbf{v}}\parallel} \parallel{\textbf{v}}\parallel = 1 \]
If \(\textbf{v}=\langle a, b\rangle\) makes an angle \(\theta\) with the positive \(x\)-axis, then \begin{equation} \label{13.vec2.compangles}\boxed{ \textbf{v} = \langle a, b\rangle = \parallel{\textbf{v}\parallel}\textbf{e}_{\textbf{v}}=\parallel{\textbf{v}}\parallel \langle \cos\theta, \sin\theta\rangle} \end{equation}
EXAMPLE 5
Find the unit vector in the direction of \(\textbf{v} = \langle 3,5\rangle\).
Solution \(\parallel{\textbf{v}}\parallel =\sqrt{3^2+5^2}=\sqrt{34}\), and thus \({\textbf{e}_{\textbf{v}} = \frac{1}{\sqrt{34}}\textbf{v} = \langle \frac3{\sqrt{34}},\frac5{\sqrt{34}}\rangle}\).
663
It is customary to introduce a special notation for the unit vectors in the direction of the positive \(x\)- and \(y\)-axes (Figure 12.17): \[ \boxed{ \textbf{i} = \langle 1,0\rangle,\qquad \textbf{j}=\langle 0,1\rangle} \]
The vectors \(\textbf{i}\) and \(\textbf{j}\) are called the standard basis vectors. Every vector in the plane is a linear combination of \(\textbf{i}\) and \(\textbf{j}\) (Figure 12.17): \[ \textbf{v} = \langle a,b\rangle = a\textbf{i}+b\textbf{j} \]
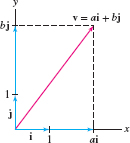
For example, \({\langle 4,-2\rangle = 4\textbf{i}-2\textbf{j}}\). Vector addition is performed by adding the \(\textbf{i}\) and \(\textbf{j}\) coefficients. For example, \[ (4\textbf{i}-2\textbf{j})+(5\textbf{i}+7\textbf{j}) = (4 + 5)\textbf{i} + (-2 + 7)\textbf{j} = 9\textbf{i}+5\textbf{j} \]
CONCEPTUAL INSIGHT
It is often said that quantities such as force and velocity are vectors because they have both magnitude and direction, but there is more to this statement than meets the eye. A vector quantity must obey the law of vector addition (Figure 12.18), so if we say that force is a vector, we are really claiming that forces add according to the Parallelogram Law. In other words, if forces \(\textbf{F}_1\) and \(\textbf{F}_2\) act on an object, then the resultant force is the vector sum \(\textbf{F}_1 +\textbf{F}_2\). This is a physical fact that must be verified experimentally. It was well known to scientists and engineers long before the vector concept was introduced formally in the 1800s.
EXAMPLE 6
Find the forces on cables 1 and 2in Figure 12.19.
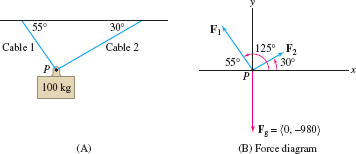
Solution Three forces act on the point \(P\) in Figure 12.19: the force \(\textbf{F}_{\mathrm{g}}\) due to gravity of \(100\mathrm{g}=980\) newtons (\(\mathrm{g}=9.8 \text{m/s}^2\)) acting vertically downward, and two unknown forces \(\textbf{F}_1\) and \(\textbf{F}_2\) acting through cables 1 and 2, as indicated in Figure 12.19.
Let \(f_1=\parallel{\textbf{F}_1}\parallel\) and \(f_2=\parallel{\textbf{F}_2}\parallel\). Because \(\textbf{F}_1\) makes an angle of \(125^\circ\) (the supplement of \(55^\circ\)) with the positive \(x\)-axis, and \(\textbf{F}_2\) makes an angle of \(30^\circ\), we can use Eq. (1) and the table in the margin to write these vectors in component form: \begin{align*}{3} \textbf{F}_1 &=& &f_1\langle \cos 125^\circ, \sin 125^\circ\rangle & &\approx f_1\langle -0.573, 0.819\rangle\\ \textbf{F}_2 &=& &f_2\langle \cos 30^\circ, \sin 30^\circ\rangle & &\approx f_2\langle 0.866, 0.5\rangle\\ \textbf{F}_{\mathrm{g}} &=& &\langle 0, -980\rangle && \end{align*}
| \(\theta\) | \(\cos\theta\) | \(\sin\theta\) |
| \(125^\circ\) | \(-0.573\) | \(0.819\) |
| \(30^\circ\) | \(0.866\) | \(0.5\) |
Now, the point \(P\) is not in motion, so the net force on \(P\) is zero: \begin{equation*} \textbf{F}_1+\textbf{F}_2 +\textbf{F}_{\mathrm{g}} = \textbf{0} \end{equation*}
664
\[ f_1\langle -0.573, 0.819\rangle + f_2\langle 0.866, 0.5\rangle + \langle 0, -980 \rangle = \langle 0, 0\rangle \]
This gives us two equations in two unknowns: \[ -0.573f_1 + 0.866f_2 = 0,\qquad 0.819f_1+0.5f_2-980 = 0 \]
By the first equation, \({f_2 = \big(\tfrac{0.573}{0.866}\big)f_1}\). Substitution in the second equation yields \[ 0.819 f_1 + 0.5\left(\frac{0.573}{0.866}\right)f_1 -980 \approx 1.15 f_1-980= 0 \]
Therefore, the forces in newtons are \[ f_1 \approx \frac{980}{1.15}\approx 852 \mathrm{N}\qquad\hbox{and}\qquad f_2 \approx \left(\frac{0.573}{0.866}\right)852 \approx 564 \mathrm{N} \]
We close this section with the Triangle Inequality. Figure 12.20 shows the vector sum \(\textbf{v}+\textbf{w}\) for three different vectors \(\textbf{w}\) of the same length. Notice that the length \(\parallel{\textbf{v}+\textbf{w}\parallel}\) varies, depending on the angle between \(\textbf{v}\) and \(\textbf{w}\). So in general, \(\parallel{\textbf{v}+\textbf{w}\parallel}\) is not equal to the sum \(\parallel{\textbf{v}}\parallel+\parallel{\textbf{w}\parallel}\). What we can say is that \(\parallel{\textbf{v}+\textbf{w}}\parallel\) is at most equal to the sum \(\parallel{\textbf{v}}\parallel+\parallel{\textbf{w}}\parallel\). This corresponds to the fact that the length of one side of a triangle is at most the sum of the lengths of the other two sides. A formal proof may be given using the dot product (see Exercise 88in Section 12.4).
THEOREM 2 Triangle Inequality
For any two vectors \(\textbf{v}\) and \(\textbf{w}\), \[ \boxed{ \parallel{\textbf{v}+\textbf{w}}\parallel\le\parallel{\textbf{v}}\parallel+\parallel{\textbf{w}}\parallel} \]
Equality holds only if \(\textbf{v}=\textbf{0}\) or \(\textbf{w}=\textbf{0}\), or if \(\textbf{w}=\lambda \textbf{v}\), where \(\lambda \ge 0\).

12.2.1 Summary
- A vector \(\textbf{v}=\overrightarrow{PQ}\) is determined by a basepoint \(P\) (the “tail”) and a terminal point \(Q\) (the “head”).
- Components of \(\textbf{v}=\overrightarrow{PQ}\) where \(P = (a_1,b_1)\) and \(Q=(a_2,b_2)\): \[ \textbf{v} = \langle a,b\rangle \] with \(a = a_2-a_1\), \(b = b_2-b_1\).
- Length or magnitude: \(\parallel{\textbf{v}}\parallel=\sqrt{a^2+b^2}\).
- The length \(\parallel{\textbf{v}}\parallel\) is the distance from \(P\) to \(Q\).
- The position vector of \(P_0=(a,b)\) is the vector \(\textbf{v}=\langle a,b\rangle\) pointing from the origin \(O\) to \(P_0\).
665
- Vectors \(\textbf{v}\) and \(\textbf{w}\) are equivalent if they are translates of each other: They have the same magnitude and direction, but possibly different basepoints. Two vectors are equivalent if and only if they have the same components.
- We assume all vectors are based at the origin unless otherwise indicated.
- The zero vector is the vector \(\textbf{0} = \langle 0,0\rangle\) of length 0.
- Vector addition is defined geometrically by the Parallelogram Law. In components, \begin{align*} \langle a_1,b_1\rangle + \langle a_2,b_2\rangle &= \langle a_1+a_2,b_1+b_2\rangle \end{align*}
- Scalar multiplication: \(\lambda \textbf{v}\) is the vector of length \(|\lambda| \parallel{\textbf{v}\parallel}\) in the same direction as \(\textbf{v}\) if \(\lambda \gt 0\), and in the opposite direction if \(\lambda \lt 0\). In components, \begin{align*} \lambda\langle a,b\rangle &= \langle \lambda a, \lambda b\rangle \end{align*}
- Nonzero vectors \(\textbf{v}\) and \(\textbf{w}\) are parallel if \(\textbf{w} =\lambda \textbf{v}\) for some scalar \(\lambda\).
- Unit vector making an angle \(\theta\) with the positive \(x\)-axis: \(\textbf{e} =\langle \cos\theta,\sin\theta\rangle\).
- Unit vector in the direction of \(\textbf{v}\ne 0\): \({\textbf{e}_{\textbf{v}} = \frac{1}{\parallel{\textbf{v}}\parallel}\textbf{v}}\).
- If \(\textbf{v} = \langle a, b\rangle\) makes an angle \(\theta\) with the positive \(x\)-axis, then \[ a = \parallel{\textbf{v}}\parallel\cos\theta,\qquad b = \parallel{\textbf{v}}\parallel\sin\theta,\qquad \textbf{e}_{\textbf{v}} = \langle \cos\theta, \sin\theta\rangle \]
- Standard basis vectors: \(\textbf{i}=\langle 1,0\rangle\) and \(\textbf{j}=\langle 0,1\rangle\).
- Every vector \(\textbf{v}=\langle a,b\rangle\) is a linear combination \(\textbf{v}=a\textbf{i}+b\textbf{j}\).
- Triangle Inequality: \({\parallel{\textbf{v}+\textbf{w}}\parallel\le\parallel{\textbf{v}}\parallel+\parallel{\textbf{w}}}\parallel\).